Domanda:
Geometria dell'anione pentacloridoindato (III)
orthocresol
2017-08-08 01:03:06 UTC
view on stackexchange narkive permalink

Secondo Brown et al. , 1 la struttura cristallina di $ \ ce {[NEt4] 2 [InCl5]} $ rivela che l'anione pentacloridoindato (III) , $ \ ce {[InCl5] ^ 2 -} $, adotta una geometria $ C_ \ mathrm {4v} $ piramidale quadrata (la teoria VSEPR predirebbe il bipiramidale trigonale $ D_ \ mathrm {3h} $):

Crystal structure of [NEt4]2[InCl5], ref 1

Secondo Greenwood e Earnshaw, 2

Si noterà che $ \ ce {[InCl5] ^ 2 -} $ non è isostrutturale con le specie isoelettroniche $ \ ce {[SnCl5] -} $ e $ \ ce {SbCl5} $, che hanno la più comune $ D_ \ mathrm {3h} $ simmetria. […] $ \ Ce {[NEt4] 2 [TlCl5]} $ è isomorfo con $ \ ce {[NEt4] 2 [InCl5]} $ e presumibilmente ha una struttura simile per l'anione.

Tuttavia, la struttura di $ \ ce {[PPh4] 2 [InCl5] .MeCN} $ è stata segnalata per avere la solita struttura bipiramidale trigonale per l'anione, 3 che getta una chiave nel lavori. Non riesco a capire molto del giornale perché è in tedesco. Dal momento che si tratta di un rapporto di una struttura cristallina, tuttavia, non mi aspetto che dica molto sulla chimica del composto.

Le differenze riportate nella geometria molecolare qui possono essere razionalizzate?

Referenze

  1. Brown, DS; Einstein, F. W. B .; Tuck, D. G. Specie di indio (III) tetragonale piramidale. Struttura cristallina del tetraetilammonio pentacloroindato (III). Inorg. Chem. 1969, 8 (1), 14-18. DOI: 10.1021 / ic50071a004.

  2. Greenwood, N. N .; Earnshaw, A. Chemistry of the Elements, 2a ed .; Butterworth – Heinemann: Oxford, Regno Unito, 1997, p 238.

  3. Bubeinheim, W .; Frenzen, G .; Müller, U. Die Chloroindate $ \ ce {[PPh4] 2 [In2Cl6]} $ und $ \ ce {[PPh4] 2 [InCl5] .CH3CN} $. Acta Crystallogr., Sez. C: Cryst. Struct. Commun. 1995, 51, 1120–1124. DOI: 10.1107 / S0108270194011789.

Hai per caso un file CIF di [Brown1969]? Oltre a [Bubenheim1995] ho appena trovato tre strutture cristalline più recenti con una $ D_ \ mathrm {3h} $ geometria trigonale quasi perfetta di $ \ ce {[InCl5] ^ {2 -}} $ e sembra che il Il lavoro di Brown è l'unico con piramide quadrata. Mi chiedo se abbia qualcosa a che fare con i dati sperimentali o il perfezionamento in quel momento - il fattore $ R $ di quasi il 10% sembra piuttosto scadente per una struttura così semplice di piccole molecole.
@andselisk no cif, mi dispiace. Immagino che potrebbe essere una possibilità, anche se non so molto di cristallografia per cominciare, quindi sono felice di sentire qualsiasi pensiero in merito.
Bene, dare un'occhiata alla struttura con checkcif.iucr.org è da dove inizierei. Come ho detto, il fattore $ R $ potrebbe essere un po 'fuori posto a causa della simmetria iniziale sbagliata e potrebbe causare la struttura sbagliata, specialmente se c'è un disturbo proposto (secondo l'articolo). Non riesco nemmeno a trovare i dati in CCDC, sebbene la voce esista. Strano, forse sono solo io a fare qualcosa di sbagliato.
Correlati: [Uso dell'indice di geometria per la determinazione dell'ambiente di coordinamento] (https://chemistry.stackexchange.com/questions/80604/use-of-geometry-index-for-the-determination-of-coordination-environment)
Una risposta:
andselisk
2017-08-08 03:55:12 UTC
view on stackexchange narkive permalink

TL; DR La struttura cristallina di $ \ ce {[NEt4] 2 [InCl5]} $ [1] inizialmente pubblicata secondo le ulteriori indagini [3], non è valida. $ \ Ce {InCl5 ^ 2 -} $ ion non ha $ C_ \ mathrm {4v} $ simmetria, e la teoria VSEPR spiega praticamente la formazione di numerosi bipiramidali trigonali leggermente distorti $ \ ce {InCl5 ^ 2 -} $ - contenenti complessi secondo i più recenti esperimenti sulla struttura monocristallina.

Dall'altro lato, le lunghezze dei legami e l'indice di geometria si riferiscono al carattere dominante di ambiente piramidale quadrato , che in questo caso può essere dettato dall'imballaggio cristallino, verso il quale $ \ ce {[InCl5] ^ 2 -} $ è più sensato di $ \ ce {[SnCl5] -} $ a causa della notevole differenza di dimensioni ($ \ ce {[InCl5] ^ 2 -} $ è più voluminoso). In ogni caso, sembra che sia necessario un altro esperimento cristallografico (preferibilmente a temperature più basse per diminuire le dimensioni degli ellissoidi termici) per determinare gli angoli in modo più preciso.

Come consiglio generale, presta sempre attenzione ai valori $ R_1 $ e $ R_2 $ della struttura cristallina. Una regola pratica: un buon affinamento della struttura di piccole molecole dovrebbe portare a $ R_1 < 0,05 $ e $ R_2 < 0,12 $.

Struttura cristallina di $ \ ce {[NEt4] 2 [InCl5 ]} $, determinato nel 1969 [1], è stato successivamente criticato in diverse pubblicazioni, coinvolgendo principalmente l'analisi aggiuntiva della vibrazione di simmetria degli spettri Raman per $ \ ce {MX5 ^ 2 -} $ anioni [2]. È stato stabilito che $ \ ce {InCl5 ^ 2 -} $ ion non ha $ C_ \ mathrm {4v} $ simmetria (ma mantiene $ C_ \ mathrm {2v} $) e che il cristallo potrebbe non essere centrosimmetrico.

I risultati sono riassunti in [3]:

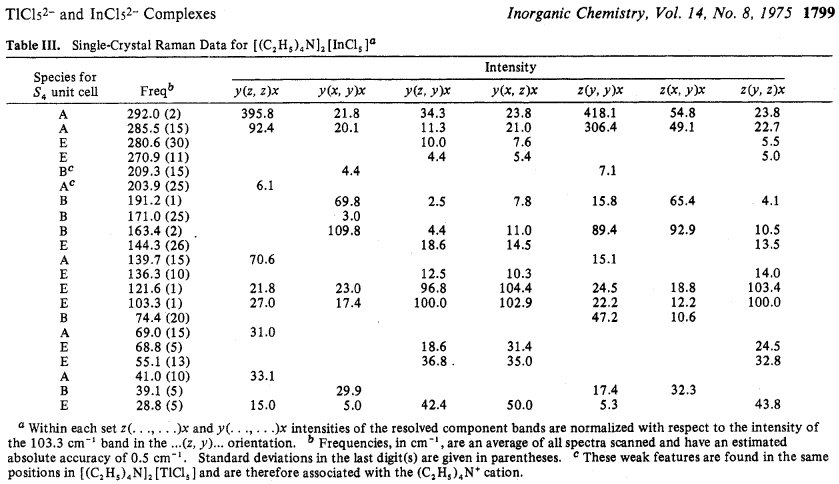
enter image description here

Deconvoluzione dei dati monocristallini è stato nuovamente eseguito con l'aiuto dei dati sulla bassa temperatura, rivelando $ 11 $ $ \ ce {InCl5 ^ 2 -} $ bande comprese tra $ 300 $ e $ \ pu {100 cm-1} $. Due allungamenti A sovrapposti sono chiaramente evidenti a $ 292 $ e $ \ pu {286 cm-1} $, ma nessun allungamento B è evidente. I due allungamenti di simmetria E previsti per l'anione di un sito $ C_2 $, ma non per un sito $ C_4 $, sono evidenti a $ 281 $ e $ \ pu {271 cm-1} $. [...] Con l'aiuto di dati a bassa temperatura, le quattro modalità E previste per $ \ ce {InCl5 ^ 2 -} $ nei siti $ C_2 $ si trovano a $ 144 $, $ 136 $, $ 122 $ e $ \ pu {103 cm-1} $ nei dati monocristallini. Con questa reinterpretazione dello spettro non è più necessario ipotizzare arbitrariamente la presenza di un modo reticolare in questa regione.

In sintesi, i dati vibrazionali per i sali di tetraetilammonio di $ \ ce {InCl5 ^ 2- } $ e $ \ ce {TlCl5 ^ 2 -} $ indicano che questi complessi risiedono su siti privi della piena simmetria $ C_4 $. La conclusione più semplice dai dati vibrazionali è che gli ioni $ \ ce {InCl5 ^ 2 -} $ hanno una simmetria $ C_2 $ locale, che sarebbe incoerente con la determinazione della struttura precedente [1]. [...]

La struttura di $ \ ce {[(C2H5) 4N] 2 [InCl5]} $, come riportato in precedenza, consisteva in $ \ ce {InCl5 ^ 2 -} $ correlati centrosimmetricamente ioni situati intorno alle posizioni c di Wyckoff di $ C_4 $ simmetria nel gruppo spaziale $ C_ \ mathrm {4h} -P4 / n $. Coassiali con gli ioni $ \ ce {InCl5 ^ 2 -} $ sono disordinati $ \ ce {(C2H5) 4N +} $ anche situati attorno alle posizioni c Wyckoff. Gli N atomi dei due rimanenti ioni $ \ ce {(C2H5) 4N +} $ nella cella unitaria occupano i siti Wyckoff b correlati centrosimmetricamente della simmetria $ S_4 $, il catione nel suo insieme è nuovamente disordinato. Ci sono due caratteristiche di disturbo di questa soluzione e del suo successivo affinamento: il disordine degli ioni $ \ ce {(C2H5) 4N +} $ e la significativa densità elettronica residua nella regione degli atomi basali di Cl del anione .

È inoltre dimostrato che per il modello ordinato l'interpretazione cristallografica più soddisfacente coesiste con la simmetria $ C_2 $ invece che con $ C_4 $. Una correlazione delle simmetrie dei punti consentite implica il passaggio da $ P4 / n $ a $ P \ bar {4} $ spazio gruppo, riducendo così il fattore $ R $ ($ R_1 $) da $ 9.5 \% $ a $ 6.7 \% $.

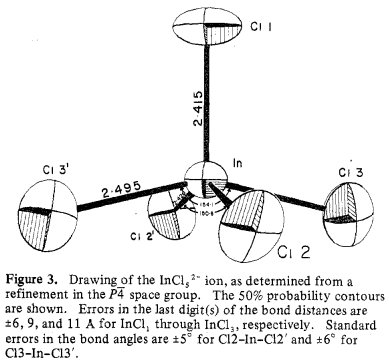
Durante il raffinamento in $ P \ bar {4} $, piccoli ma significativi cambiamenti si verificano nel piano basale di $ \ ce {InCl5 ^ 2 -} $ ion . Gli atomi basali di Cl si sono spostati di $ \ pu {-0,5 A} $ dalla loro quadruplice posizione simmetrica in $ P4 / n $, portando a variazioni nelle distanze di legame e negli angoli attorno all'atomo In (Figura 3) che sono qualitativamente sufficienti per spiegare i risultati vibrazionali.

enter image description here

Indice di geometria $ \ tau_5 $ per $ \ ce {[InCl5]} $ fragment può essere utilizzato per determinare l'ambiente di coordinamento formale come segue:

$$ \ tau_5 = \ frac {\ beta - \ alpha} {60 ^ \ circ}, $$

dove $ \ alpha $, $ \ beta $ - i due maggiori angoli di valenza del centro di coordinamento ($ \ angle \ ce {Cl - In - Cl} $, $ \ alpha < \ beta $).

\ begin {align} \ begin {cases} \ tau_5 & = 0 \ qquad & \ text {square pyramidal geometry} \\\ tau_5 & = 1 \ qquad & \ text {trigonal bipyramidal geometry} \ end { case} \ end {align}

Per la struttura $ \ ce {[NEt4] 2 [InCl5]} $ originale rifinita in [3] ho preso i valori angolari dai loro materiali supplementari. Si è scoperto che cambiare il gruppo spaziale in $ P \ bar {4} $ risulta ancora nel carattere dominante della geometria piramidale quadrata di $ \ ce {[InCl5] ^ 2 -} $, anche se bisogna ricordare che l'asse di rotazione dell'ordine più elevato è $ C_2 $, non $ C_4 $:

$$ \ alpha = (150.6 \ pm 5.0) ^ \ circ, \ beta = (154.1 \ pm 6.0) ^ \ circ, \ bar {\ tau_5} = \ frac {154,1 ^ \ circ - 150,6 ^ \ circ} {60 ^ \ circ} = 0,06; \ tau_5 \ in [0,04; 0.24] $$

L'articolo [4] menziona che per le strutture isoelettroniche $ \ ce {[SnCl5] -} $ - continenti con vari cationi sono state riportate solo geometrie trigonali-bipiramidali e suggerisce una maggiore influenza dell'impaccamento dei cristalli su $ \ ce {[InCl5] ^ 2 -} $ geometria. Ciò può anche essere spiegato dalla maggiore flessibilità del frammento $ \ ce {MX5} $ in $ \ ce {[PPh4] 2 [InCl5]} $ rispetto a $ \ ce {[PPh4] [SnCl5]} $ [5] dovuto a una lunghezza media del legame maggiore: $ d (\ ce {In - Cl}) = \ pu {2.5 A} $, $ d (\ ce {Sn - Cl}) = \ pu {2.3 A} $.

Per quanto riguarda i dati sperimentali ausiliari, tutte le strutture cristalline compreso il frammento $ \ ce {[InCl5] ^ 2 -} $ determinato negli ultimi due decenni supportano completamente la teoria VSEPR che predice la simmetria $ D_ \ mathrm {3h} $ bipiramidale trigonale ( con un'eccezione intermedia di $ \ tau_5 \ approx 50 \% $).

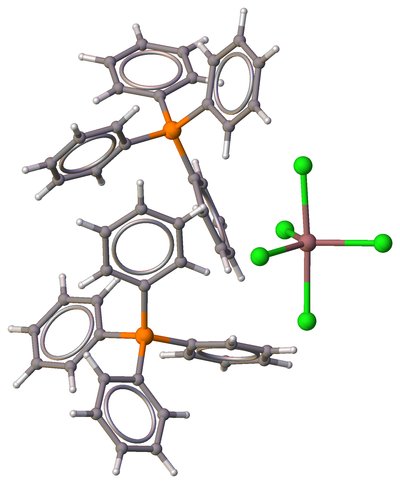
  1. bis (Tetraphenylphosphonium) pentacloroindato (III) [4], geometria bipiramidale trigonale: $$ \ alpha = 124,24 ^ \ circ , \ beta = 174,74 ^ \ circ, \ tau_5 = \ frac {174,74 ^ \ circ - 124,24 ^ \ circ} {60 ^ \ circ} = 0,84 $$

    $ \ color {#EEEEEE} { \ Large \ bullet} ~ \ ce {H} $; $ \ color {# 909090} {\ Large \ bullet} ~ \ ce {C} $; $ \ color {# FF8000} {\ Large \ bullet} ~ \ ce {P} $; $ \ color {# 1FF01F} {\ Large \ bullet} ~ \ ce {Cl} $; $ \ color {# A67573} {\ Large \ bullet} ~ \ ce {In} $.

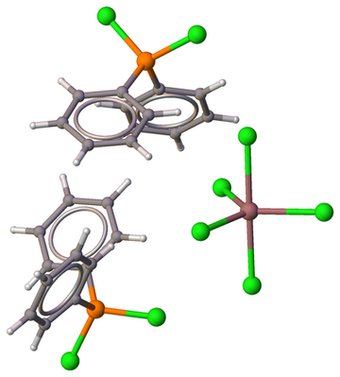
    enter image description here

  1. bis (difenildiclorofosfonio) pentacloroindato (III) [6], geometria bipiramidale trigonale: $$ \ alpha = 120,93 ^ \ circ, \ beta = 179,29 ^ \ circ, \ tau_5 = \ frac {179,29 ^ \ circ - 120,93 ^ \ circ} {60 ^ \ circ} = 0.97 $$

    $ \ color {#EEEEEE} {\ Large \ bullet} ~ \ ce {H} $; $ \ color {# 909090} {\ Large \ bullet} ~ \ ce {C} $; $ \ color {# FF8000} {\ Large \ bullet} ~ \ ce {P} $; $ \ color {# 1FF01F} {\ Large \ bullet} ~ \ ce {Cl } $; $ \ color {# A67573} {\ Large \ bullet} ~ \ ce {In} $.

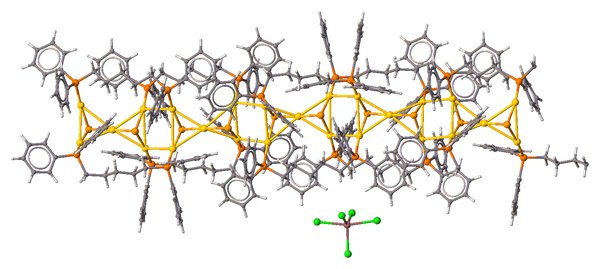
    enter image description here

    1. tetrakis ($ \ mu_3 $ -Selenido) -tetrakis ($ \ mu_2 $ -1,5-bis (difenilfosfino) pentano) -deca-oro (I) pentacloroindato (III) [7], geometria intermedia: $$ \ alpha = 138,45 ^ \ circ, \ beta = 166,50 ^ \ circ, \ tau_5 = \ frac {166,50 ^ \ circ - 138,45 ^ \ circ} {60 ^ \ circ} = 0,47 $$

      $ \ color {#EEEEEE} {\ Large \ bullet} ~ \ ce {H} $; $ \ color {# 909090} {\ Large \ bullet} ~ \ ce {C} $; $ \ color {# FF8000} {\ Large \ bullet} ~ \ ce {P} $; $ \ color {# 1FF01F} {\ Large \ bullet} ~ \ ce {Cl} $; $ \ color {# FFA100} {\ Large \ bullet} ~ \ ce {Se} $; $ \ color {# A67573} {\ Large \ bullet} ~ \ ce {In} $; $ \ color {# FFD123} {\ Large \ bullet} ~ \ ce {Au} $.

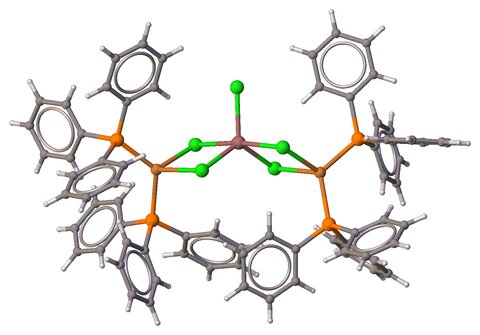
      enter image description here

    1. tetrakis ($ \ mu_2 $ -chloro) -cloro-tetrakis (trifenilfosfina-P) -di-rame (I) -indium (III) tetraidrofurano solvato [8], geometria bipiramidale trigonale (sebbene gli autori si riferiscano ad essa come a "quasi "coordinazione piramidale quadrata basata su un singolo $ \ ce {In - Cl} $ distanza di legame $ (d (\ ce {In-Cl_ \ mathrm {ap}}) = \ pu {2.36 A}) $, più breve $ d (\ ce {In-Cl_ \ mathrm {eq}}) = \ pu {2.42 A}) $: $$ \ alpha = 123.90 ^ \ circ, \ beta = 172.89 ^ \ circ, \ tau_5 = \ frac { 172,89 ^ \ circ - 123,90 ^ \ circ} {60 ^ \ circ} = 0,82 $$

      $ \ color {#EEEEEE} {\ Large \ bull et} ~ \ ce {H} $; $ \ color {# 909090} {\ Large \ bullet} ~ \ ce {C} $; $ \ color {# FF8000} {\ Large \ bullet} ~ \ ce {P} $; $ \ color {# 1FF01F} {\ Large \ bullet} ~ \ ce {Cl} $; $ \ color {# C88033} {\ Large \ bullet} ~ \ ce {Cu} $; $ \ color {# A67573 } {\ Large \ bullet} ~ \ ce {In} $.

      enter image description here

    Bibliografia

    1. Brown, DS; Einstein, F. W. B .; Tuck, D. G. Inorganic Chemistry 1969 , 8 (1), 14-18. DOI 10.1021 / ic50071a004.
    2. Adams, D. M .; Smardzewski, RR Journal of the Chemical Society A: Inorganic, Physical, Theoretical 1971 , 714. DOI 10.1039 / j19710000714.
    3. Joy, G .; Gaughan, A. P .; Wharf, I .; Shriver, D. F .; Dougherty, J. P. Inorganic Chemistry 1975 , 14 (8), 1795-1801. DOI 10.1021 / ic50150a011.
    4. Bubenheim, W .; Frenzen, G .; Müller, U. Acta Crystallographica sezione C 1995 , 51 (6), 1120–1124. DOI 10.1107 / S0108270194011789.
    5. Müller, U .; Siekmann, J. F. Acta Cryst C 1996 , 52 (2), 330–333. DOI 10.1107 / S0108270195011073.
    6. Taraba, J .; Zak, Z. Inorganic Chemistry 2003 , 42 (11), 3591–3594. DOI 10.1021 / ic034091n.
    7. Olkowska-Oetzel, J .; Sevillano, P .; Eichhöfer, A .; Fenske, D. European Journal of Inorganic Chemistry , 2004 (5), 1100-1106. DOI 10.1002 / ejic.200300774.
    8. Zhang, X.-Z .; Song, Y.-W .; HuiWu, F .; Zhang, Q.-F. Zeitschrift für Naturforschung B 2007 , 62 (6). DOI 10.1515 / znb-2007-0605.
Certamente non la risposta che mi aspettavo, ma comunque eccellente. Grazie!
@orthocresol Non so cosa c'era di sbagliato in me ieri sera, ma ho calcolato erroneamente $ \ tau_5 $ per il tuo complesso ($ \ alpha $ improprio da SI), le mie sincere scuse. In realtà supporta la geometria piramidale quadrata anche per la struttura rifinita per la seconda volta, sebbene a causa della simmetria ridotta non si possa attribuire $ C_ \ mathrm {4v} $. Ho modificato la risposta in modo corrispondente aggiungendo qualche dettaglio in più. Probabilmente potresti voler deselezionarlo come accettato (o addirittura downvote), poiché nuovi dati sperimentali o calcoli QC potrebbero essere più significativi dell'idea dell'effetto di impaccamento dei cristalli qui proposta.
Nessun problema. Bene, generalmente, se arrivano nuove informazioni, la risposta accettata può sempre essere cambiata, quindi IMO non è un grosso problema. Il downvoting sarebbe crudele, no? ;)
@orthocresol Ebbene, è stata comunque colpa mia e le colpe dovrebbero essere punite / ignorate, non premiate. Ma grazie per il simpatico atteggiamento!


ⓘ
Questa domanda e risposta è stata tradotta automaticamente dalla lingua inglese. Il contenuto originale è disponibile su stackexchange, che ringraziamo per la licenza cc by-sa 3.0 con cui è distribuito.
Loading...