Se vuoi davvero capire perché i livelli di energia dei sistemi $ \ pi $ coniugati sono come sono, ti suggerisco di dare una buona occhiata alla teoria di Hückel come suggerito da @ssavec: questo metodo è solo un'approssimazione ma per la sua semplicità è davvero utile per aiutarti a comprendere i concetti sottostanti. Tuttavia, facendo come hai suggerito e guardando la sovrapposizione complessiva tra gli orbitali $ \ text {p} $ in un dato orbitale molecolare lo fa davvero sembrano funzionare anche se non ho una giustificazione rigorosa per questo.

Dalla teoria di Hückel è noto che i coefficienti degli orbitali $ \ text {p} $ in un dato orbitale molecolare possono essere calcolati come

\ begin {equation} c_ {j, r} = \ sqrt {\ frac {2} {N + 1}} \ sin \ Bigl (\ frac {rj \ pi} {N + 1} \ Bigr) \ end {equation}

fornendo il coefficiente $ c_ {jr} $ per l'atomo $ j $ nell'orbitale molecolare $ r $ di un sistema coniugato di $ N $ atomi (così che $ j $ e $ r = 1, 2, 3, \ dots, n $).

Applichiamo questo al butadiene.

Il $ \ p i $ orbitali molecolari del butadiene sono $ \ Psi_ {1} $, $ \ Psi_ {2} $, $ \ Psi_ {3} $ e $ \ Psi_ {4} $. Sono costruiti da una combinazione lineare di 4 atomici $ \ text {p} $ orbitals ($ \ phi_ {1} $, $ \ phi_ {2} $, $ \ phi_ {3} $ e $ \ phi_ {4} $), quindi

\ begin {equation} \ Psi_ {r} = c_ {1, r} \ phi_ {1} + c_ {2, r} \ phi_ {2} + c_ {3, r} \ phi_ {3} + c_ { 4, r} \ phi_ {4} \ end {equation}

Quando si calcolano i coefficienti orbitali atomici per ciascun orbitale molecolare $ r $, si arriva alla seguente immagine:

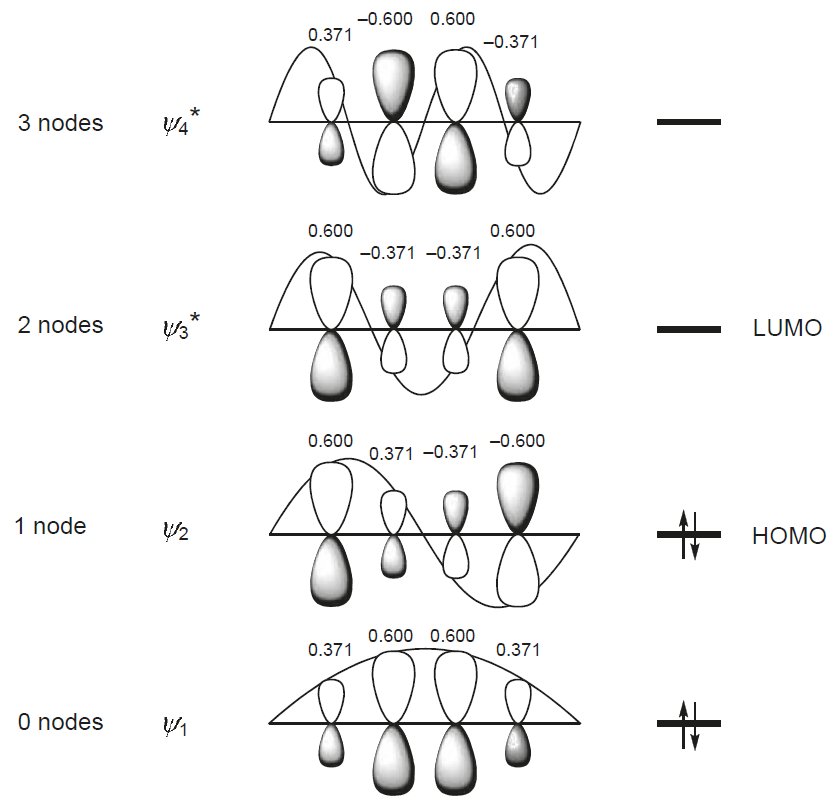
dove i numeri sopra i diversi $ \ text {p} $ orbitali sono i coefficienti.

Facendo lo stesso per l'etene si ottiene quanto segue:

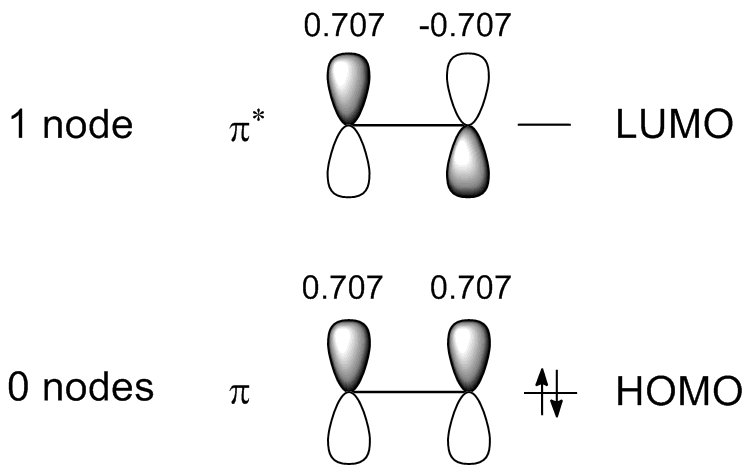
Ora, è necessario confrontare la sovrapposizione complessiva negli HOMO di etene e butadiene Poiché è già assunta nella teoria di Hückel, viene considerata solo la sovrapposizione tra gli orbitali $ \ text {p} $ vicini. Inoltre, è utile impostare l'integrale di sovrapposizione di due $ \ text {p} $ orbitali "normali" (entrambi con coefficiente $ c = 1 $) a 1 (il suo valore esatto non ha importanza perché solo la quantità relativa di sovrapposizione in diversi MO sono importanti per questo confronto), in modo da poter calcolare la sovrapposizione complessiva in un orbitale molecolare semplicemente moltiplicando i coefficienti degli orbitali $ \ text {p} $ vicini e sommando questi prodotti. Quindi, per la sovrapposizione nel etene e butadiene HOMO ottieni:

\ begin {align} S _ {\ text {HOMO, ethene}} & = 0.707 \ cdot 0.707 \\ & = 0.500 \\ \\ S _ {\ text {HOMO , butadiene}} & = 0.600 \ cdot 0.371 + 0.371 \ cdot (-0.371) + (-0.371) \ cdot (-0.600) \\ & = 0.307 \ end {align}

C'è meno sovrapposizione e quindi meno legame nell'HOMO del butadiene rispetto all'HOMO dell'etene, il che implicherebbe che l'HOMO del butadiene ha un'energia più alta di quella dell'etene.

Ora, che dire dei LUMO:

\ begin {align} S _ {\ tex t {LUMO, ethene}} & = 0.707 \ cdot (-0.707) \\ & = -0.500 \\ \\ S _ {\ text {LUMO, butadiene}} & = 0.600 \ cdot (-0.371) + (-0.371) \ cdot (-0.371) + (-0.371) \ cdot 0.600 \\ & = -0.307 \ end {align}

C'è più sovrapposizione e quindi più legame (o meglio dire meno antilegame) nel LUMO del butadiene rispetto al LUMO dell'etene, il che implicherebbe che il LUMO del butadiene è inferiore in termini di energia rispetto a quello dell'etene.

Quindi, l'HOMO del butadiene è più elevato in termini di energia di quello dell'etene e del LUMO di butadiene ha un'energia inferiore a quella dell'etene, quindi il divario HOMO-LUMO nel butadiene è inferiore a quello nell'etene.

Ecco un approccio alternativo per rispondere a questa domanda utilizzando l'approccio "Particle in a Box". Il livello di energia $ N ^ {th} $ per una particella in un riquadro unidimensionale è dato da $$ E_n = \ frac {n ^ 2h ^ 2} {8mL ^ 2} $$ dove h è la costante di Planck, m il massa della particella e L la lunghezza della scatola. L'energia del livello di energia N + 1 è uguale a $$ E_ {n + 1} = \ frac {(n + 1) ^ 2h ^ 2} {8mL ^ 2} $$. Sottraendo questi due termini si ottiene la separazione energetica tra questi due livelli di energia come $$ \ Delta E = \ frac {(2n + 1) h ^ 2} {8mL ^ 2} = K \ frac {2n + 1} {L ^ 2} $$. Nella foto sotto è rappresentato l'inizio della nostra serie di polieni, etilene, butadiene, esatriene ...

Per semplicità, supponiamo che tutte le lunghezze dei legami siano uguali. Quindi la "lunghezza" della nostra scatola aumenta di 2L ogni volta che passiamo da etilene a butadiene a esatriene, ecc. Se ora confrontiamo la differenza di $ \ Delta E $ ($ \ Delta \ Delta E $) per $ N ^ {th} $ e $ (N + 1) ^ {st} $ livelli di energia tra etilene e butadiene, troviamo che la differenza nella separazione dei livelli di energia è data da $$ \ Delta \ Delta E = K (2n + 1 ) (\ frac {1} {L ^ 2} - \ frac {1} {9L ^ 2}) = K '(\ frac {8} {9L ^ 2}) $$ Se eseguiamo lo stesso confronto per butadiene e esatriene vediamo che $$ \ Delta \ Delta E = K (2n + 1) (\ frac {1} {9L ^ 2} - \ frac {1} {25L ^ 2}) = K '(\ frac {16} {225L ^ 2}) $$ e per l'esatriene rispetto all'ottatetraene è $$ \ Delta \ Delta E = K (2n + 1) (\ frac {1} {25L ^ 2} - \ frac {1} {49L ^ 2}) = K '(\ frac {24} {1225L ^ 2}) $$ In altre parole, quando aumentiamo la lunghezza della nostra scatola (aumentiamo la lunghezza del nostro poliene), la separazione energetica tra qualsiasi coppia corrispondente di livelli di energia (HOMO-LUMO è un caso) si ridurrà. Spero che questo aiuti!