Nota: puoi saltare la sezione I e andare direttamente alla sezione II e / o alla fine della sezione III (in particolare la sottosezione delle conclusioni), se hai già familiarità con le definizioni / meccanismi matematici di base
I. Preliminari
Sentiti libero di saltare tutto questo se lo conosci
Primo, abbiamo un ' espansione adiabatica , ovvero $ \ mathrm {q} = 0 $.
In secondo luogo, il nostro processo viene eseguito come segue: un gas alla pressione $ p_i $ fluisce in una regione di pressione inferiore $ p_f $ senza significative cambiamento nell'energia cinetica. Questa è chiamata espansione Joule – Thomson .
Ovviamente, questo processo è intrinsecamente irreversibile. Inoltre, si può mostrare che questa espansione èenthalpic (cioè $ H_i = H_f $). A differenza di un'espansione libera, il lavoro viene svolto, provocando un cambiamento nell'energia interna; le specifiche esatte di questo cambiamento dipenderanno dalle condizioni iniziali e finali e anche dalla natura del fluido di lavoro.
Ciò che misuriamo sperimentalmente è un cambiamento di temperatura rispetto alla pressione a $ H $ costante, e lo chiamiamo $ \ mu _ {\ mathrm {JT}} $ (coefficiente di Joule-Thomson).
$$ \ mu _ {\ mathrm {JT}} = \ left (\ frac {\ partial T} {\ partial P} \ right) _H = \ frac {V (T \ alpha-1)} { C_p} \ tag {1} $$
dove $ \ alpha $ è il coefficiente di espansione termica $$ \ alpha = \ frac {1} {V} \ left (\ frac {\ partial V} {\ partial T} \ right) _p $$
Tutti i gas reali hanno un punto di inversione in cui il valore di $ \ mu _ {\ mathrm {JT}} $ cambia segno. La temperatura di inversione di Joule – Thomson, dipende dalla pressione del gas prima dell'espansione.
$$ \ begin {array} {cc} \ hline \ text {Temperature} & \ text {sign of} \ \ P parziale & \ text {segno di} \ \ mu _ {\ mathrm {JT}} & \ text {quindi segno di} \ \ parziale T \\ \ hline \ text {sotto la temperatura di inversione} & - & + & - \\\ text {above inversion} & - & - & + \\ \ hline \ end {array} $$
La pressione finale è sempre inferiore alla pressione iniziale e quindi la variazione è sempre negativa. A seconda che tu sia al di sopra o al di sotto della temperatura di inversione, il tuo cambiamento di temperatura può essere positivo (riscaldamento) o negativo (raffreddamento). Vorrei sottolineare che la temperatura di inversione dipende sia dalla temperatura che dalla pressione.
II. Analisi qualitativa
Gli argomenti forniti di seguito potrebbero sembrare un po '"ondeggianti" / rozzi, ma abbiate pazienza.
$$ H = U + pV $$$$ \ Delta H = \ Delta U + \ Delta (pV) $$
Durante un'espansione di Joule-Thomson (isentalpica, adiabatica), la modifica in $ pV $ rappresenta il lavoro svolto da il fluido.
Se $ PV $ aumenta, a entalpia costante, allora U deve diminuire come risultato del fluido che lavora nei suoi dintorni; il materiale di lavoro utilizza la propria energia interna per svolgere il lavoro. Questo produce una diminuzione della temperatura e si traduce in un coefficiente di Joule-Thomson positivo.
La diminuzione di $ pV $ significa che si lavora sul fluido e l'energia interna aumenta. Questo può quindi portare ad un aumento della temperatura e il coefficiente di Joule-Thomson sarà negativo.
Per un gas ideale, $ pV $ non cambia durante un'espansione di Joule-Thomson.
Di conseguenza, non vi è alcun cambiamento nell'energia interna; inoltre, non ci sono variazioni di temperatura; e il coefficiente di joule-thomson è zero.
Nei gas reali, $ pV $ cambia. La deviazione dall'idealità (in generale) è contenuta in $ Z $, il fattore di compressibilità. Quindi, avrebbe senso se potessimo stabilire una connessione ad esso.
Il rapporto tra il valore di $ pV $ "reale" e quello previsto per un gas ideale alla stessa temperatura è chiamato fattore di compressibilità ,
$$ Z: = \ frac {pV} {nRT} $$
Per un gas, questo è tipicamente inferiore all'unità a bassa temperatura (forze attrattive dominanti) e maggiore dell'unità ad alta temperatura.
A bassa pressione, il valore di $ Z $ si sposta sempre verso l'unità man mano che un gas si espande (tende all'idealità).
In generale a bassa temperatura, $ Z $ e $ PV $ aumenteranno con l'espansione del gas, determinando un coefficiente di Joule-Thomson positivo.
Ad alta temperatura, $ Z $ e $ pV $ diminuiscono con l'espansione del gas; se la diminuzione è abbastanza grande, il coefficiente di Joule-Thomson sarà negativo.
Ne consegue che per $ Z>1 $, il coefficiente di Joule-Thomson sarà negativo e il gas si riscalda. Questo è il caso dei gas in questione alle condizioni date.
Un grafico da wikipedia che mostra come il coefficiente di Joule-Thomson cambia segno (per l'azoto):
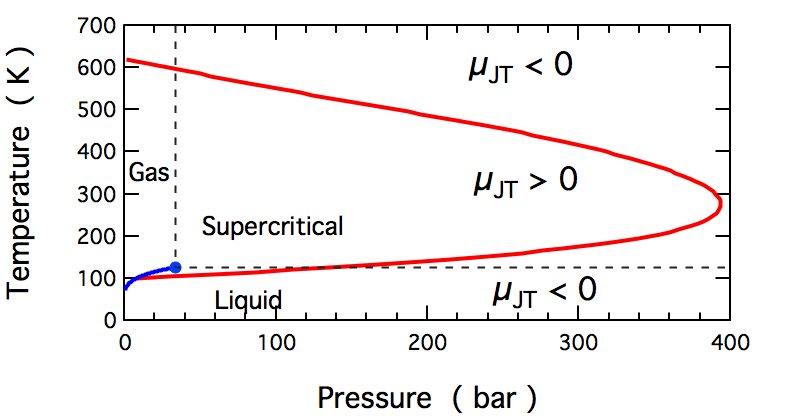
Nota: la domanda originariamente posta sui gas, ma farò un piccolo punto sulle fasi condensate e sui fluidi supercritici (dato che puoi vederli nel grafico). A pressioni elevate, queste fasi non possono rispondere a un aumento della pressione riducendone il volume e $ pV $ aumenta all'aumentare della pressione. Le molecole vengono forzate insieme e tale coefficiente di Joule-Thomson è negativo.
Ovviamente le forze intermolecolari, attraenti e repulsive, e i limiti in cui sono dominanti sono fondamentali per spiegare il modifiche di $ Z $ e di conseguenza di $ \ mu _ {\ mathrm {JT}} $. Questo punto è ulteriormente sviluppato nella sezione successiva.
III. Un'analisi leggermente più quantitativa, ma in definitiva qualitativa
Per vedere come entrano in gioco le interazioni intermolecolari, diamo un'occhiata a due sistemi modello: un gas ideale (senza interazioni intermolecolari) e un gas di Van der Waals (entrambi attraenti e interazioni repulsive).
Usando l'equazione (1) e la definizione di $ \ alpha $ possiamo scrivere
$$ \ mu _ {\ mathrm {JT}} = \ frac {V (T \ alpha -1)} {C_p} = \ frac {T \ left (\ left (\ frac {\ partial V} {\ partial T} \ right) _p -V \ right)} {C_p} \ tag {2} $$
Per un gast perfetto $ \ left (\ frac {\ partial V} {\ partial T} \ right) _p = \ frac {V} {T} $ e così, $ \ mu _ {\ mathrm {JT}} = 0 $
Poiché l'equazione dei gas di Van der Waals è cubica in $ V $, userò i primi pochi termini dell ' espansione viriale e risolverò $ V $ per ottenere $ \ left (\ frac { \ partial V} {\ partial T} \ right) _p $. Sto omettendo calcoli espliciti, puoi eseguirli come esercizio.
$$ Z = 1 + \ frac {1} {RT} \ left (b- \ frac {a} {RT} \ right ) p + .... \ tag {3} $$
Poiché $ Z = \ frac {p \ tilde {V}} {RT} $ dove $ \ tilde {V} $ è il molare volume del gas; Lo faccio per comodità, non voglio portarmi dietro un $ n $ dappertutto.
$$ \ tilde {V} = \ frac {RT} {p} + \ left (b- \ frac {a} {RT} \ right) + .... \ tag {4} $$
Dopo la differenziazione otteniamo
$$ \ left ( \ frac {\ partial V} {\ partial T} \ right) _p = \ frac {R} {p} + \ left (- \ frac {a} {RT ^ 2} \ right) + .... \ tag {5} $$
Sostituendo (4) e (5) in (2) e eliminando tutti i termini di ordine superiore.
$$ \ mu _ {\ mathrm {JT }} \ approx \ frac {\ frac {2a} {RT} -b} {C_p} $$
Ora, considera il limite di bassa temperatura di questa espressione. $ \ Frac {2a} {RT} $ diventa grande e $ b $ è trascurabilmente piccolo rispetto ad esso quindi
$$ \ mu _ {\ mathrm {JT}} \ approx \ frac {2a} {RTC_p} $$
Tutte le quantità sul lato destro di questa equazione sono positive. quindi $ \ mu $ è positivo. Le forze attrattive sono dominanti, poiché nella nostra espressione compare solo il parametro $ a $.
Allo stesso modo, il limite di alta temperatura è
$$ \ mu _ {\ mathrm {JT}} \ approx \ frac {-b} {C_p} $$
Qui $ \ mu $ è chiaramente negativo. Le forze repulsive sono dominanti, poiché nella nostra espressione compare solo il parametro $ b $.
Conclusioni
- L'esistenza di una temperatura di inversione diventa ovvio in un gas con forze sia attrattive che repulsive, poiché $ \ mu _ {\ mathrm {JT}} $ cambia segno da positivo a negativo.
- Anche la connessione con forze attrattive e repulsive diventa più esplicita.
- Nel limite di bassa temperatura, le forze attrattive sono dominanti e il gas deve liberarsi da queste interazioni mentre si espande. Ciò richiede energia, che deve essere fornita da $ U $ l'energia interna del gas. Così il gas si raffredda.
- A temperature elevate, le repulsioni sono dominanti. Man mano che il gas si espande, il potenziale eccessivo viene ridotto e l'energia viene rilasciata. Pertanto, il gas si riscalda.
- Ovviamente, l'entità esatta del limite di temperatura alto e basso dipende dalla natura del fluido di lavoro, poiché il i parametri $ a $ e $ b $ sono diversi per ogni gas. I gas di cui parli hanno interazioni a malapena attraenti.
Avvertenze
- La nostra analisi basata sul Van der Waals gas sembra suggerire che la temperatura di inversione e $ \ mu_ \ mathrm {JT} $ sia una funzione determinata dalla sola temperatura. Ciò ha dimostrato sperimentalmente di essere falso . Questa discrepanza sorge perché nella nostra espansione abbiamo abbandonato i termini di ordine superiore che contenevano la dipendenza dalla pressione.
- Questo modello è in definitiva qualitativo. Ti darà i numeri sbagliati quando provi a calcolare qualcosa, ma spiega bene le tendenze generali.