Bene, il primo passo è smettere di pensare gli elettroni come se fossero palline molto piccole che orbitano attorno al nucleo in un percorso circolare. Questo è noto come il modello di Bohr. Nonostante questo modello sia un modello eccellente a livello introduttivo, non racconta l'intera storia.

Ci sono diversi problemi con l'idea che gli elettroni viaggino in un'orbita circolare attorno al nucleo, la principale è che alla fine dovrebbero subire un decadimento orbitale e quindi alla fine rallentare e schiantarsi nel nucleo. Ovviamente questo non accade. Allora come si muovono gli elettroni intorno al nucleo?

È qui che la teoria quantistica venne in soccorso all'inizio del XX secolo. Affermava che gli elettroni non potevano essere trattati come una particella classica e non avevano una posizione e una quantità di moto definite. Quindi questo significa fondamentalmente che non possiamo conoscere esattamente la posizione di un elettrone e la sua quantità di moto allo stesso tempo. Questa relazione è data dal Principio di incertezza di Heisenberg .

Non entrerò nei dettagli al riguardo poiché per mantenere questa spiegazione di base, ma se sei interessato guarda questo video che fornisce un'ottima spiegazione.

Quindi, in pratica, cosa ci dice la teoria quantistica che in realtà non possiamo specificare dove e quale percorso prenderà un elettrone. Tuttavia il modello di Bohr presume che tu possa tracciare con precisione dove sarà un elettrone, ma ora sappiamo che a causa del principio di indeterminazione di Heisenberg non puoi conoscere con precisione la posizione e la quantità di moto esatte di un elettrone. Quindi in realtà non possiamo costruire un'orbita e dire che l'elettrone seguirà sempre quel percorso.

Pertanto, rende impossibile tracciare un'orbita per un elettrone come puoi? Se non sai dove sarà l'elettrone, non c'è modo di prevederne il percorso.

Allora come possiamo aggirare questo problema? Bene, se non possiamo disegnare l'orbita di un elettrone, la prossima cosa migliore che possiamo fare è tracciare un orbitale di probabilità di densità elettronica per esso. Noto anche come orbitali atomici .

Un orbitale è una regione dello spazio ben definita. Pertanto un orbitale atomico è una regione dello spazio che mostra dove sarà l'elettrone per il 95% delle volte (di solito prendiamo il 95% ma potrebbe essere qualsiasi numero come il 90% o il 75%).

Un modo semplice di pensare agli orbitali è immaginare di avere una fotocamera magica in grado di scattare una sequenza di foto di un elettrone in un atomo di idrogeno. L'elettrone appare come un punto. Ora, se sovrapponiamo tutte queste immagini, vedrai qualcosa di simile:

Dato che generalmente consideriamo gli orbitali atomici come regione dello spazio che mostra dove sarà l'elettrone per il 95% delle volte, si dice che la sfera più esterna dell'immagine sopra sia l'orbitale dell'elettrone.

Spera che questo ti aiuti a capire gli orbitali. Se hai qualche domanda, sentiti libero di chiedere.

Perché non provi con analogie: almeno, come introduzione di base varia, apprezzo molto il tentativo fatto qui da Goh et al.

Un orbitale è definito come una regione nello spazio in cui c'è un'alta probabilità di trovare un elettrone. Un'analogia per un orbitale è la possibile posizione di uno studente in base al suo orario. Ad esempio, secondo l'orario, lunedì alle 9.00, uno studente deve essere in Aula 1 per una lezione di chimica. Si può dire che, per un periodo di settimane, c'è un'alta probabilità che questo studente si trovi nell'aula 1 a quell'ora in quel giorno. Tuttavia, non si può essere sicuri al 100% che questo studente sarà lì perché potrebbe essere assente da scuola quel giorno. Inoltre, di solito non si può prevedere esattamente dove siederà lo studente nell'aula, ma si può dire, con un'alta probabilità che questo studente si troverà entro i confini dell'aula. Questa analogia descrive abbastanza bene un orbitale, perché prende in considerazione la probabilità e la regione dello spazio nella definizione di un orbitale.

Inizierò sicuramente con tale un'analogia che sembra fornire una descrizione abbastanza semplice, sebbene completa, di come dovrebbero essere considerati gli orbitali.

Ok. Dimentica per un secondo tutto ciò che riguarda gli orbitali.

Hai dei nuclei. Hai elettroni intorno a loro.

Primo passo: gli elettroni non sono sfere. Immaginali come una carica imbrattata nello spazio. Che è precisamente quello che sono: carica imbrattata nello spazio, con bordi sfocati, come un blob sfocato. La forma di questo blob dipende da molti fattori, ma il più grande è la posizione dei nuclei.

Ora supponi di voler descrivere la forma di questo blob, come se volessi stamparlo in 3D. Un modo semplice sarebbe dividere lo spazio in cubetti e dire "carica" ​​se hai qualche sbavatura o "nessun addebito" se non hai quella macchia. In pratica, poiché è sfocato, direste "carica 3.0" in alcuni cubi, "carica 1.3" in altri cubi, "carica 0.1" in altri cubi e così via. Questo è un modo perfettamente legittimo per descrivere quella che viene chiamata "densità di carica" ​​nello spazio.

Il problema con questo approccio è che è piuttosto scomodo. Ha una scarsa precisione e scala male. Se riduci i cubetti, perché non ti piace vivere in un mondo di Minecraft, hai bisogno di molti più cubi per farlo.

Quindi ora c'è un metodo più intelligente per farlo e per spiegare ho bisogno che tu capisca la decomposizione di Fourier. Non è così difficile come pensi che suoni.

Il problema è il seguente. Hai un'onda sonora complessa, come quella prodotta soffiando un fischio o cantando una canzone, e risulta che puoi creare qualsiasi forma complessa di questa onda sommando insieme onde più semplici: un'attenta scelta di seno e coseno di determinate frequenze (toni) e con determinate intensità (volumi). Suonali tutti insieme, ottieni indietro l'onda iniziale.

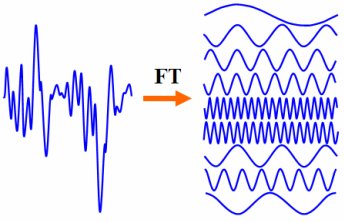
Questo è esattamente quello che vedi nel display dello spettro nel tuo stereo

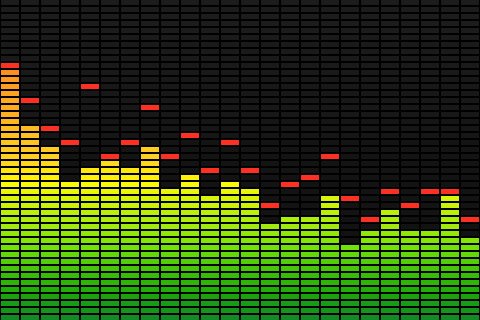
Dove ogni colonna è una frequenza diversa e l'altezza della colonna è l'intensità di quella particolare frequenza. Cambia continuamente perché stai suonando musica complessa, ma prova a suonare un suono uniforme (ad esempio un violino che suona una singola nota) e vedrai che rimane lo stesso per tutto il tempo.

Ora torna agli orbitali .

Gli orbitali sono i "seno e coseno" del nostro problema di descrivere quel blob. Abbiamo un'entità complessa (il nostro blob spalmato) e vogliamo descriverla sommando "qualcosa". Non importa quale "qualcosa" usiamo, ma risulta che le funzioni tridimensionali di quella forma hanno molte proprietà interessanti che rendono il problema molto più compatto.

Facciamo un semplice esempio. Supponi di avere una carica sferica. Questo è probabilmente descritto bene da un singolo orbitale di forma sferica (un orbitale s), esattamente come un'onda sinusoidale di un diapason è ben descritta da una singola funzione seno.

Ora aggiungi un campo elettrico in modo che il gli elettroni vengono tirati e la sfera imbrattata è ora più simile a un uovo allungato. Quella non è davvero descritta bene da una sfera, vero? quindi devi descrivere il lobo, il che significa che hai bisogno di un orbitale aggiuntivo (ap orbitale) da aggiungere al mix in modo che il risultato sia a forma di uovo, esattamente come se avessi bisogno di più di un'onda sinusoidale per descrivere il suono di un violino.

Questo è tutto, davvero. gli orbitali sono solo convenienti equivalenti 3d del seno e del coseno. Potremmo anche usare qualsiasi altra cosa (e in effetti lo facciamo, in alcuni casi) e funzionerebbe anche, ma con alcuni potenziali svantaggi.

La spiegazione della struttura orbitale atomica di un atomo è una storia affascinante. È stato appena risolto negli ultimi cento anni. Non è stato un viaggio lineare, ma un viaggio pieno di ogni sorta di vicoli ciechi e viaggi secondari. I greci pensavano che gli elementi fossero aria, fuoco, acqua e terra. Non comprendendo l'atomo gli alchimisti trascorsero miliardi di ore e una quantità infinita di denaro cercando di trasformare altre sostanze in oro.

Quindi il primo passo significativo nella risoluzione della struttura atomica inizia con Dmitri Mendeleev a cui è attribuita la nozione di tavola periodica. Ciò ha consentito la scoperta di elementi aggiuntivi necessari per completare la tabella. Tuttavia, il motivo per cui la disposizione del tavolo funzionava era sconosciuto.

Più o meno nello stesso periodo stavano svolgendo altri lavori. Maxwell ha creato le sue famose equazioni che collegano corrente elettrica e magnetismo.

La scoperta dell'elettrone è avvenuta più o meno nello stesso periodo. Ma fu solo intorno al 1900 che la comprensione di un elettrone era abbastanza completa.

I fisici ancora non capivano come mettere insieme un atomo. A questo punto molti modelli atomici furono lanciati per spiegare vari fenomeni. Uno di questi modelli era il plumb pudding. L'idea era che un atomo fosse come una goccia di budino in cui gli elettroni erano sospesi come prugne nel budino.

Un grande passo avanti venne dalla diffusione di Rutherford intorno al 1910. Questi esperimenti hanno dimostrato che il nucleo (carica positiva) si trovava al centro di un atomo e che aveva un volume molto piccolo rispetto all'intero atomo. Questo ha portato al modello planetario dell'atomo. Gli elettroni caricati negativamente orbitavano intorno al nucleo caricato positivamente come i pianeti in orbita attorno al sole.

Questo non spiegava altri fenomeni noti come spettri lineari dell'idrogeno che Balmer aveva scoperto prima del 1900.

Tali spettri di linea erano correlati tramite la formula di Rydberg che metteva in relazione il numero quantico principale $ n $ con la struttura atomica.

$ \ frac {1} {\ lambda} = R (\ frac {1} {{n_1} ^ 2} - \ frac {1} {{n_2} ^ 2}) $

nel 1913 fu sviluppato il modello Bohr. Questo spiegava che gli elettroni erano disposti in gusci e il riempimento della struttura di guscio poteva essere ricollegato alla tavola periodica!

La struttura della shell è fondamentalmente attaccata al modello planetario da Arnold Sommerfeld e l'idea era che per qualsiasi motivo gli elettroni non potevano ruotano intorno al nucleo dell'atomo in "qualsiasi" orbita ma che dovevano occupare certe orbite che divennero note come conchiglie. Al modello di Bohr sono state aggiunte delle sottostrutture ($ l $, $ m $ e $ s $) per confondere orbite aggiuntive per spiegare la sottile struttura spettroscopica di alcuni elementi. Come le linee di Fraunhofer osservate negli spettri del sole.

Quindi a questo punto fisici e chimici avevano catalogato gran parte del comportamento degli atomi, ma ancora non avevano una completa comprensione di come gli atomi lavorato.

A metà degli anni '20 Schrödinger sviluppò la sua famosa equazione che completava il puzzle della struttura degli atomi negli elettroni e nel nucleo più fondamentali. Dal modello di Bohr si è capito che gli elettroni devono trovarsi in certe orbite perché le orbite sono quantizzate. Vale a dire che ogni orbitale ha un'energia specifica. Quello che Schrödinger ha mostrato è che le orbite non erano come le corsie di un evento di atletica leggera che limitava gli elettroni, ma che l'orbita dell'elettrone era distribuita in una nuvola 3D attorno all'atomo. Un altro aspetto del lavoro di Schrödinger e altri era che l'elettrone aveva sia caratteristiche d'onda e caratteristiche particellari.

Utilizzando l'equazione delle onde di Schrödinger è stato possibile calcolare la forma degli orbitali. Ora questo era nel 1930 il lasso di tempo che i computer erano ancora lontani decenni. Quindi questi calcoli sono stati fatti a mano! Il "problema" era che risolvere le equazioni era possibile solo per un elettrone. Utilizzando il calcolo è bello essere in grado di risolvere equazioni in modo che gli integrali possano essere facilmente calcolati. Tuttavia il problema dei tre corpi non consente una tale soluzione. Con i computer moderni è possibile calcolare soluzioni numeriche anche se gli integrali non esistono.

Quindi torniamo alla domanda. Un orbitale è una funzione matematica che descrive il percorso 3D di un elettrone attorno al nucleo. Piuttosto che un planetario come "orbita", l'orbitale è una funzione di probabilità. La densità dell'orbita varia in funzione del raggio. A seconda dell'orbitale, la funzione di probabilità mostra anche un orientamento nello spazio 3D. Quindi un orbitale S è sferico in quanto non c'è preferenza X-Y-Z. gli orbitali P sebbene non solo abbiano un aspetto radiale ma abbiano orientamenti spaziali. Quindi i tre orbitali P sono come le rotazioni 3D di una rosa a due foglie nello spazio 2D. Quindi gli orbitali P hanno lobi orientati lungo l'asse +/- x, l'asse +/- y e l'asse +/- z.

Una parola di cautela. Le rappresentazioni orbitali sono molto utili per prevedere il comportamento chimico, ma non sono "reali". Questo ovviamente diventa un po 'folle quando si formano quattro orbitali molecolari $ sp ^ 3 $ ciascuno con il 25% di carattere S e il 75% di carattere P! È un po 'come pensare che un unicorno sia un ibrido di cavallo e rinoceronte.

Non conosco abbastanza la fisica per sapere se questo è sul bersaglio o meno, ma ...

L'idea di differenti modalità vibrazionali è facile da dimostrare con una grande ciotola d'acqua e il dito. Riempi la ciotola e usa il dito per eccitare diversi modelli di onde stazionarie sulla superficie.

Inizia dal centro della ciotola, muovi il dito lentamente su e giù e dovresti essere in grado di ottenere un onda stazionaria radialmente simmetrica che assomiglia a una versione bidimensionale di un orbitale 1S. Una volta trovata la frequenza fondamentale, raddoppiala e otterrai qualcosa come un orbitale 2S. Spostati fuori centro e probabilmente puoi eccitare una modalità che assomiglia a 1P e 2P.

Sfortunatamente, dovrai fermarti qui, perché le modalità di ordine superiore sul bidimensionale superficie dell'acqua non ha molta somiglianza con gli orbitali tridimensionali di ordine superiore.

Ma quello che puoi mostrare, è che le onde stazionarie nello spazio ristretto del bowl sono limitati a pochi tipi possibili distinti e che per ogni tipo la frequenza sembra essere sempre un multiplo intero di una frequenza fondamentale.

L'orbitale è una funzione d'onda di un elettrone. Descrive dove ci si deve aspettare un elettrone (o una coppia, se necessario), ignorando in qualche modo tutti gli altri elettroni.

Un elettrone è sia una particella che un'onda.

Le onde sonore che viaggiano nell'aria libera possono avere qualsiasi frequenza. Ma un disco vibrante può risuonare solo a determinate frequenze. Questi corrispondono alle modalità di vibrazione del disco. Le animazioni in fondo a https://en.wikipedia.org/wiki/Vibrations_of_a_circular_membrane mostrano queste modalità di vibrazione e c'è una corrispondenza uno a uno con gli orbitali di simmetria s, pe d (simmetrie orbitali più complesse richiedono 3 dimensioni.)

Sebbene questa analogia sia lungi dall'essere perfetta, mostra i principi di una funzione d'onda. Nota che in tutti i casi tranne 1s, c'è una parte della membrana che non si muove affatto. Questo è chiamato nodo. I nodi possono essere planari o circolari / sferici. In un orbitale, un nodo è un luogo in cui la probabilità di trovare un elettrone è zero.

Il numero totale di zone in cui la probabilità di trovare un elettrone è zero (questo include la zona di distanza infinita dal atomo) è dato dal numero nella designazione orbitale. Il numero di nodi planari è dato dalla lettera.

Quindi tutti gli orbitali con designazione 3 hanno 3 zone in cui la probabilità di trovare un elettrone è zero. 3s ha 2 nodi sferici (la 3a zona è a distanza infinita dall'atomo). 3p ha un nodo planare e 1 nodo sferico. 3d ha 2 nodi planari (dandogli la familiare forma a 4 lobi). Nota anche che c'è un orbitale 3d con un nodo conico, ma lo considereremo come appartenente allo stesso gruppo delle note planari.

Tornando all'analogia del disco circolare, vediamo che può vibrare in una serie di modi discreti e il suo movimento può essere descritto come una combinazione di questi modi.

In un atomo, il principio di esclusione di pauli impone che tutti gli elettroni debbano avere numeri quantici diversi. Pertanto ogni orbitale può contenere fino a 2 elettroni, a condizione che abbiano spin diversi. In questo modo l'atomo differisce dall'analogia del disco vibrante, in quanto il disco può vibrare con qualsiasi ampiezza, ma un orbitale può contenere solo 0,1 o 2 elettroni.

Ogni elettrone ha una certa energia, a seconda da quale orbitale si trova. L'energia dell'elettrone dipende anche dalla sua interazione con altri elettroni in altri orbitali. In gran parte a causa di queste interazioni, troviamo che gli orbitali con più nodi planari hanno un'energia più alta di quelli con meno nodi planari.

Immagina che fossi tuo fratello minore, come gli spiegheresti un orbitale? (supponendo che sappia cosa sono gli atomi di elettroni e neutroni e il resto delle nozioni di base fino a quel punto).

C'è un po 'di problema lì, in quanto probabilmente non saprà cosa gli elettroni sono. Non esiste un modello di elettroni nel modello standard. È descritta come una particella fondamentale, ma non esiste una descrizione reale di come viene creata nella produzione di coppie gamma-gamma o di cosa sia realmente. Puoi trovare informazioni su spinori e cintura di Dirac e sull ' equazione di Dirac, che è un'equazione d'onda. Ma poi si parla di particelle puntiformi e probabilità e tutto diventa confuso.

Ho letto su questo e non riesco a capirlo.

IMHO è facile quando fai un po 'di lavoro investigativo . Dai un'occhiata all'articolo di Wikipedia sugli orbitali atomici e nota che gli elettroni "esistono come onde stazionarie" . Il punto controverso è che quando si estrae un elettrone da un orbitale atomico, ancora esiste come un'onda stazionaria. Lo hai fatto insieme a un positrone di fotoni nella produzione di coppie gamma-gamma. Puoi diffrangere gli elettroni. Diffrazione elettronica "si riferisce alla natura ondulatoria degli elettroni" . L'elettrone è un'onda . Un'onda permanente . Onda stazionaria, campo stazionario. L'elettrone non orbita attorno al nucleo come un pianeta, è più simile a un anello elettromagnetico di Saturno. Non è piatto, è sferico, ma è difficile da immaginare, quindi nel descriverlo al tuo fratellino, usa un anello piatto. Per mostrarglielo, dagli uno sparkler e convincilo a ruotarlo in tondo. Questo crea un'immagine a forma di anello, che si riferisce all'orbitale s di seguito:

_{Immagine per gentile concessione di UCDavis Chemwiki}

Ora fagli ruotare la candela a forma di otto. Ciò si riferisce all'orbitale p nell'orientamento x y o z. Quindi convincilo a ruotare la scintilla in modo da quadrifoglio. Ciò si riferisce a un orbitale d e così via.

Tra l'altro come si relazionano i diversi livelli di energia con essi.

Perché abbiamo a che fare con le onde elettromagnetiche piuttosto che con le stelle filanti, e i livelli di energia sono un po 'come gli ingranaggi. Guarda questa immagine di Kenneth Snelson:

C'è sempre un numero intero di lunghezze d'onda nell'onda stazionaria. L'atomo è un "oscillatore armonico quantistico". L'onda elettronica può effettivamente cambiare marcia quando assorbe un'onda fotonica E = hf. Quando emette un fotone, cambia effettivamente marcia.

Ovviamente gli orbitali degli elettroni non sono così semplici, ma dovrebbero allontanare il tuo fratellino dalla prima base.

Non cercherò di spiegare cosa "un orbitale" "sia" al mio ipotetico fratellino più di quanto farei a un cane. SE ci fosse qualche motivo per spiegarli, allora dovrei sapere di cosa si tratta. Ho notato che non hai nemmeno menzionato se stavi parlando di orbitali atomici o orbitali molecolari ... Se spinti, direi che gli orbitali descrivono la forma del volume di spazio in cui l'elettrone legato con un dato insieme di numeri quantici è molto probabile che sia la forma dello spazio in cui l'elettrone trascorre la maggior parte del suo tempo.

Gli oribitali sono i luoghi in cui gli elettroni si depositano in un atomo stabile. Questo si basa su due emisferi della forza debole "nucleomagnetica" di tipo magnetico sottostante dal nucleo a ciascun elettrone che mantiene gli elettroni in un guscio. Questa forza è repulsiva quando la carica elettrostatica è attraente. Capisco perché gli elettroni rimangono nel campo.

Di conseguenza, ottieni i primi punti di bilanciamento del guscio alle estremità dei due assi. Quindi, Hyrogen con uno e Helium con due, quindi il subshell e il guscio sono pieni.

Dopodiché, gli elettroni riempiono due emisferi crescendo per quadrati, quindi il guscio successivo sono due subshell. Questa di una piramide che costruisce 1/3/5/5/3/1 da polo a equatore a polo. Nota che 1 + 3 + 5 = 9 che essendo un quadrato perfetto. Tuttavia, questi sono in due emisferi, quindi subshell di dimensioni 2, 6, 10. E le conchiglie complete sono 2x1, 2x4, 2x9.

Vedi il mio libro su Scrunched Cube Atomic Model per spiegare conchiglie e subshell per la gente comune.